Algebra de Conjuntos

La Teoría de Conjuntos era novedosa cuando yo estudiaba el bachillerato, pues se salía de las matemáticas tradicionales que habían aprendido nuestros antepasados. De hecho, algún compañero de colegio, de “Letras”, denominación de la época para aquellos que abandonaban las matemáticas, física y química a los catorce años, en oposición  a los de “Ciencias”, que dejábamos el latín a esa misma edad, confiesa, todavía, que no la entendió nunca.

Sin entrar en profundidad en dicha teoría, conviene recordar que dice  que un conjunto A se puede definir como una agrupación, clase o colección de objetos denominados elementos del conjunto. Estos elementos tienen carácter individual,  tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: a, b, c,...

De esta manera, si A es un conjunto, y  a, b, c, d  todos sus elementos, es común escribir:

A = {a,b,c,d} 

para definir tal conjunto A

El conjunto universal, que siempre representaremos con la letra U, es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos de ciudades, U es el conjunto de todas las ciudades, este conjunto universal puede mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el contexto que estemos tratando, pero siempre es necesario demostrar la existencia de dicho conjunto previamente.

Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por Ø.

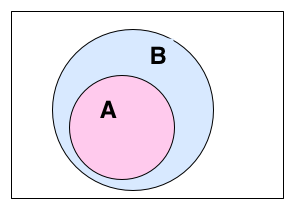
Un conjunto A se dice que es subconjunto de otro B, si cada elemento de A es también elemento de B.

Así, el conjunto vacío es subconjunto de todo conjunto A y todo conjunto A es subconjunto del conjunto universal.

Las principales operaciones entre conjuntos son la unión, la intersección y la diferencia. Si queréis ver algo más, podéis ir aquí.

Os estaréis preguntando a que se debe esta disquisición matemática sobre algo tan árido. Como decía al principio, hace treinta o cuarenta años, la teoría de conjuntos podía considerarse una novedad, pero hoy ya no, sin embargo, veo que mucha gente que ocupa puestos de responsabilidad no tiene la menor idea de algo tan elemental.

Así, ayer, Ibarretxe, como en muchas otras ocasiones, ha dicho que el recurso, presentado por el Gobierno,  ante el Tribunal Constitucional, para impedir la consulta soberanista impulsada por el lendakari, “…rompe las relaciones entre el España y Euskadi (debería decir, en castellano, País Vasco o Vascongadas), reflejadas en el Estatuto de Guernica…”

Habría que explicarle, a él y a todos los que le aplauden, que el País Vasco es un subconjunto de España y que, por tanto, las relaciones de la comunidad vasca  con la nación española es una relación de dependencia constitucional como la del resto de las regiones y, él, no puede convocar referéndums desde el gobierno regional y tiene que entender que la soberanía reside en el conjunto del pueblo español y no en el subconjunto vasco.

Habría que recordarle también a él y a otros nacionalistas separatistas como él, que con sus ideas anexionistas de convertir el País Vasco en un conjunto universal, al final, lo que van a llegar a ser es un conjunto vacío.